Меню
Вхід і реєстрація

Математика «по Петерсон» широко известна не только в России. В декабре 2018 года учебник Людмилы Георгиевны для начальной и основной школы успешно прошёл все необходимые экспертизы и по многочисленным просьбам учителей и родителей вновь вернулся в федеральный перечень. В начале учебного года мы попросили её рассказать, как помочь ребёнку с математикой, как заинтересовать ею взрослых и почему детям важно чувствовать свой успех.
Сначала оговоримся, что «посредственное преподавание» — термин весьма условный. У всех родителей и педагогов разное представление о том, каким оно должно быть. Но в целом я понимаю, что вы имеете в виду: допустим, ребёнок приходит из школы с потухшими глазами, а при одном слове «математика» у него возникает стойкое отвращение.
Давайте попробуем понять, почему детей невозможно оторвать, например, от компьютеров, в отличие от изучения математики. Что их так притягивает в компьютерных играх? Мне кажется, срабатывают несколько факторов:
Этот набор факторов в достаточной степени обеспечивает механизм мотивации «надо» — «хочу» — «могу». Чтобы заинтересовать ребёнка математикой, можно действовать по аналогии.

Желание заниматься любым делом возникает только в атмосфере взаимного уважения, доверия и доброжелательности. Без близких отношений с детьми родители мало чем могут им помочь, кроме покупки еды, одежды и канцтоваров.
Очень важно понять, что именно вызывает у ребёнка нежелание заниматься. Для этого нужен спокойный безоценочный разговор. Ребёнок должен быть уверен, что вы его спрашиваете не для того, чтобы оценить или дать наставление, а чтобы помочь справиться с тем, что пока не получается.

Дайте ему возможность выговориться. Подумайте вместе о причинах, из-за которых математика перешла в разряд нелюбимых предметов. Всегда легче всё списать на «посредственное преподавание» или на что-то ещё внешнее, что не требует работы над собой. Но это не поможет решить проблему, скорее наоборот. Чтобы вдохновить ребёнка к работе над собой, нужно искренне верить в него и не уставать повторять, что у него всё получится.
Это не значит оставаться равнодушным к его результатам. Напротив, адекватная реакция родителей на неуспех — это сопереживание и соучастие: «Давай разберёмся, что пока не получилось». Двигаться вперёд помогает не нотация, а осознание своих проблем.
Каждый ребёнок развивается в индивидуальном темпе, поэтому значение имеет не столько результат, сколько динамика относительно самого себя.
Любое усилие — это уже маленькая победа. Верно выполненное задание — ещё один шаг. Получилось то, что раньше не получалось, — следующий
Очень важно замечать и фиксировать любое движение вперёд, даже самое незначительное. Тогда ребёнок почувствует, что он не обвиняемый, родители с ним на одной стороне, они — его друзья и поддержка.
Осознание ребёнком того, что пока не получается, поможет подвести его к новой цели. В учёбе это всегда узнать то, что он пока «не знает», научиться тому, что ещё «не умеет». Именно поэтому так важно понять, что конкретно вызывает трудности. Приведу пример подводящего диалога. Предположим, он говорит, что ничего не понимает в математике.
— Совсем ничего? Давай полистаем учебник, тетрадь.
— Такие задания ты умеешь делать? А такие?
Рассматривая учебник вместе с ребёнком, нужно показать сначала самые простые задания, потом — посложнее. И так до тех пор, пока не встретится действительно непонятное. Дальше надо вместе подумать, как выполнять такие задания.
— Отлично! Ты разобрался в том, чему надо научиться (цель). А теперь давай подумаем, как это можно сделать?
Важно дать ребёнку высказаться, выслушать его варианты, подсказать возможности, которые он не назвал. Их может быть много. Например, подойти к учителю, спросить у друга или старшей сестры, разобраться по учебнику самому или вместе с вами.

Главное — наметить план действий и довести его до успешного результата. Дайте ребёнку поверить в себя, обязательно обратите внимание на то, что получилось: «Вот это круто, а говорил — не умеешь!»
Конечно же, ребёнка любого возраста и любого уровня подготовки полезно вовлекать в решение игровых и нестандартных задач. Начинать всегда лучше с малого. Подбросьте задачку, с которой он точно справится, а потом ещё одну, посложнее.
Сейчас в интернете можно найти огромное количество интересных задач любой сложности, не ограничиваясь, разумеется, только нашим учебником. Например, замечательные книги Я. Перельмана «Занимательная математика», «Весёлые задачи», «Быстрый счёт», «Живая математика»; Б. Кордемского «Математическая смекалка»; А. Калининой, Е. Кац, А. Тилипман «Математика в твоих руках», задачи-мультики из TED и многие другие.
Не торопите, не хмыкайте, если он даёт неверный ответ. Восхититесь его достижениями: «Надо же, а я не догадался! Здорово!»
Если у ребёнка горят глаза, когда он рассказывает о задаче, которую смог решить, то он готов к постановке более высоких целей — сначала участие, а затем и победы в разных математических олимпиадах. Их сейчас, помимо Всероссийской олимпиады школьников, множество, очных и онлайн. Главное — следить за тем, чтобы не пропадал интерес, а уровень и темп были для него посильны.
Ребёнок всегда будет стремиться только к тому, что у него получается. Нам всем, как вода для жизни, необходима ситуация успеха. Педагог Василий Сухомлинский писал: «Моральные силы для преодоления своих слабых сторон ребёнок черпает в своих успехах».
При этом успех не связан напрямую с отметками. Например, можно получить пятёрку за списанную работу. Порадоваться нечему. А можно, приложив усилия, дотянуться до тройки — это настоящая победа! Её формула: «затруднение — усилие в его преодолении — успех». Чем больше было усилие, тем радостнее победа.

Взрослые часто хвалят ребёнка лишь за отметки. Мне кажется, гораздо важнее наблюдать за его усилиями, динамикой, достижением намеченных целей и делить с ним радость побед.
Потребность в признании и уважении окружающих — это одна из базовых потребностей любого человека. Признание порождает уверенность в себе, желание достигать результата, значимого для окружающих.
Поэтому так важно внимание семьи к успехам. Расскажите о победах ребёнка бабушке и дедушке. Вспомните и порадуйтесь во время семейного обеда или на прогулке. Этим вы не только поддержите желание заниматься математикой, но и поможете ребёнку воспитать уважение к себе.
Эти простые правила — лишь некоторая модель, следование которой не навредит. Конечно, важно, чтобы математика была интересна самому родителю: пользы будет тем больше, чем больше он ею увлечён. Ведь вряд ли можно увлечь тем, что тебе неинтересно самому.
Сейчас таких взрослых становится всё больше. Недавно мне попалась книга профессора математики Университета Твенте в Голландии Нелли Литвак в соавторстве с Аллой Кечеджан «Математика для безнадёжных гуманитариев», которая и родилась как ответ на этот запрос взрослых. Авторы, узнав, как много у книги читателей, создали для них в фейсбуке группу «Математика — великая и ужасная». Сейчас она насчитывает десятки тысяч участников и постоянно растёт.

Это только один пример, но можно порекомендовать и много других прекрасных книг. Например, «Большой роман о математике. История мира через призму математики» Микаэля Лонэ. Эта книга выходит в серии «Удовольствие от науки» и помогает понять, насколько математика интересная и захватывающая. Автор рассказывает об истории этой науки с древности до наших дней и о том, какой она станет через десятки, сотни лет.

Существует также много увлекательных видеороликов и фильмов самых разных жанров, которые вдохновляют на изучение математики. Например, ролики «Мы и математика», «Природа в числах», фильмы «Великая тайна математики», «Доказательство», «Умница Уилл Хантинг», «Чувственная математика», «Х+Y», «Любимое уравнение профессора», «Человек, который познал бесконечность», «Тайный знак», «Софья Ковалевская», «Двадцать одно», «Игра на понижение», «Вселенная Стивена Хокинга», «Бесконечность», «Агора», «Пи», «Математика и черт», «I.Q.», «Игры разума».
В интернете есть множество лекций и целостных курсов математики для взрослых, в том числе бесплатных. За пару часов каждый может построить собственную траекторию математического развития. Лучший сценарий — изучать её вместе с детьми, открывать с ними новые математические понятия и формулы, решать интересные задачи, шутить и радоваться успехам. А главное — общаться с ними и заниматься общим делом, на что у родителей сегодня часто не хватает времени и в чём так нуждаются дети.
Возвращение учебников в ФПУ, без сомнения, сняло гигантскую проблему, которая мешала работать тысячам школ и детских садов. Не только потому, что учителя снова без проблем могут использовать учебники. Главное, что восстановилась справедливость по отношению к блестящим педагогам, подготовившим за много лет не одно поколение успешных и талантливых детей.
Планов у нас, как всегда, очень много. Для всех педагогов, работающих по нашему непрерывному курсу математики «Учусь учиться», будут проходить бесплатные ежемесячные онлайн-консультации по всем классам.

В сентябре планируем запустить проект «Умный решебник». Это образовательная онлайн-платформа, где дети и родители смогут не только найти готовые решения к заданиям нашего курса, но и самостоятельно разобраться в причинах затруднений, связанных с решением тех или иных задач.
Мы продолжаем работу Федеральной инновационной площадки и Всероссийского исследовательского проекта, который сегодня объединяет более четырёх тысяч педагогов — лидеров в своих регионах. В этом году Всероссийский проект стал международным. В рамках этих площадок мы разрабатываем и тестируем новые направления для решения проблем, волнующих сегодня всех: как системно и эффективно формировать умение учиться, как измерить и оценить метапредметные результаты образования, как перевести школы с так называемыми низкими результатами обучения в режим развития, как построить интересную для детей систему олимпиадной подготовки по математике с 1-го по 9-й класс. Мы ищем ответы на эти и другие вопросы: создаём образовательные программы и технологии, апробируем их в школах и детских садах.

У нас работает и «Детская академия» — это центр дополнительного математического образования для дошкольников с пяти лет и школьников с 1-го по 5-й класс, один из наших молодых проектов. Мы помогаем каждому ребёнку найти свой ответ на вопрос «Зачем мне учить математику?».
Каждый ученик в нашей «Детской академии» проходит комплексный мониторинг склонностей, по результатам которого наши специалисты вместе с самим ребёнком и его родителями составляют индивидуальный маршрут его обучения. Занятия в «Детской академии» больше напоминают увлекательные квесты, где каждый может двигаться в своём темпе по выбранному маршруту.
Дети работают в разновозрастных группах — играют, экспериментируют, строят математические модели, решают в командах проектные задачи. Под каждую группу занятие собирается с помощью специального «конструктора», учитывающего возраст, интересы, особенности детей этой группы. Таким образом, мы реализуем идеи персонализированного обучения (в том числе и в рамках онлайн-образования).

Да, это ключевой вопрос. От его решения, на мой взгляд, будет зависеть конкурентоспособность школы в будущем. Всё больше родителей ждут, чтобы детям было интересно учиться, чтобы у них росла вера в свои силы, накапливался опыт личных и коллективных побед, чтобы они были готовы к саморазвитию и осознанно выбирали свой путь — вместе с приобретением новых знаний. Всё это достигается метапредметными результатами образования, навыками XXI века.
Для этого нужны новые методы обучения. Однако на практике педагоги часто предпочитают просто объяснять детям темы. Причина ясна. Любая структура, добиваясь эффективности, ориентируется на результат, за который отчитывается. В нашем случае это в основном административные контрольные работы, средний балл ВПР, ОГЭ и ЕГЭ. Эти результаты в той или иной мере достигаются привычным тренингом.
Зачем же педагогам что-то менять? Ведь объяснить детям материал гораздо проще, чем подвести их к самостоятельному открытию
Реальный переход к новой школе требует новых измерителей результатов образования. Сейчас этим направлением занимаются многие, в том числе и мы — как теоретическими исследованиями, так и прикладными разработками в рамках надпредметного курса «Мир деятельности».
Уже сегодня существуют разные варианты критериев и мониторинга метапредметных умений, но пока все они в стадии апробации. Впереди ещё большая работа по их уточнению и совершенствованию.
ЕГЭ, как и любой экзамен, конечно же, не только про знания, но и про трудолюбие, ответственность, умение выстроить стратегию своей подготовки, справиться с волнением, сосредоточиться и многое другое. Однако итоговый результат ЕГЭ, с моей точки зрения, не даёт достаточной информации о качестве образования.
Каков был начальный уровень ребёнка и какова динамика его роста? Что он умеет делать сам — без репетиторов и наставников? Умеет ли работать в команде? Какие у него интересы и увлечения? Насколько он стрессоустойчив, если что-то пошло не так? Какие у него цели и планы и как он их ставит и описывает?
Ответы на эти и многие другие вопросы, как мне кажется, не менее важны для оценки результатов, чем полученный на ЕГЭ балл. Более того, именно эти вопросы в первую очередь будут интересовать будущих работодателей наших выпускников.
Поэтому для меня очевидно, что ЕГЭ со временем будет меняться и дополняться, чтобы соответствовать требованиям нашей жизни.
Самое точное определение математики дал, с моей точки зрения, великий Анри Пуанкаре: «Математика — это искусство называть разные вещи одним и тем же именем». В этом определении соединились и сущность математического языка — обобщённое описание закономерностей окружающего мира, — и то волшебство и красота, которые несут в себе математические законы. Альберт Эйнштейн всегда удивлялся и восхищался тем, как легко и понятно математика описывает Вселенную.
Возьмём простой ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… В нём каждое число, начиная с третьего, равно сумме двух предыдущих. Эту последовательность построил Леонардо Фибоначчи более семи веков назад. И вот оказалось, что именно этими числами выражается, как правило, количество лепестков на цветах. Как это может быть?

Но это не всё. Последовательность чисел Фибоначчи наглядно можно изобразить с помощью спирали. Эту форму мы неожиданно найдём в природе на совершенно не связанных между собой объектах: спирали улитки, спирали Галактики, спирали на срезе кочана капусты, в соцветии подсолнуха, эту же форму имеют вихри и циклоны.
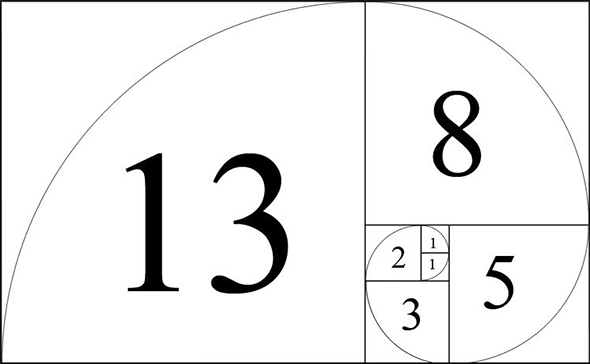

Почему так? Почему отношение чисел в золотом сечении, которое описывает одновременно и пропорции человеческого тела, и расположение листьев на стебле цветка, и правила гармонии в живописи, архитектуре, дизайне, которым уже более 4000 лет, — всё это напрямую связано с отношением соседних чисел ряда Фибоначчи? Неужели возможно этому не удивиться?
Для меня красота математики связана прежде всего с глубиной и универсальностью её законов
Если, например, случайным образом выбрать 1000 человек и построить график их распределения по росту, то получится кривая Гаусса, где верхняя точка графика будет соответствовать среднему росту в группе. Чем больше людей будет в выборке, тем более эстетически совершенная линия будет получаться. Известный английский учёный Фрэнсис Гальтон сказал: «Если бы древние греки знали закон нормального распределения Гаусса, они бы его обожествили».
Математика — живая, развивающаяся наука. Сегодня, конечно же, она описывает далеко не все явления мира, и это означает, что впереди нас ждут удивительные математические открытия. Мы хотим, чтобы дети осваивали эту науку как часть культуры, поэтому главная задача — помочь им увидеть математику в её развитии, прочувствовать красоту и глубину её законов.
Для этого важно создавать среду, в которой дети могут сами совершать открытия — сталкиваться с неизвестным, испытывать вдохновение, выдвигать свои идеи, переживать победы и неудачи, удивляться и восхищаться логикой математики и красотой математических законов. Свою задачу мы видим в том, чтобы создавать для этого педагогические инструменты — технологии, методики, новое содержание математического образования.
Теги: начальная школа , образование , сучасна школа
Приєднуйтесь до нашої сторінки у Facebook
«Освіта Нова» — у вашій стрічці новин